Moses’s Missing Math
This is a Voronoi diagram:

The colored regions identify every point in the image that is closer to the black dot inside the region than to any other black dot. So, for example, all the purple points near the center of the image are closer to that black dot than they are to any other.
This is Deuteronomy 21:1–4:
“If in the land that the LORD your God is giving you to possess someone is found slain, lying in the open country, and it is not known who killed him, then your elders and your judges shall come out, and they shall measure the distance to the surrounding cities. And the elders of the city that is nearest to the slain man shall take a heifer that has never been worked and that has not pulled in a yoke. And the elders of that city shall bring the heifer down to a valley with running water, which is neither plowed nor sown, and shall break the heifer’s neck there in the valley.”
Moses is trying to help define justice in a world where atonement for sin requires the blood of animals, but sometimes a terrible sin—like murder—is discovered without a perpetrator. In this passage, he’s answering the question, “What if a person is found murdered out in the wilderness, and we can’t find the murderer? How do we pay the price for that sin?”
You may be wondering, “Why must anyone pay the price? Surely the murderer will face justice in this life or the next.”
But there’s a problem: there’s no CSI: Jerusalem. So the murderer will probably never be found. And Moses knows that the whole of Israel must remain pure in the eyes of the Lord as a condition of remaining in the Promised Land. Individual sin becomes corporate sin if it’s not appropriately atoned. The adage “one bad apple spoils the barrel” is quite literally true, and the consequences are exile and death.
So you figure out which city is closest to the random spot in the wilderness, and that city’s elders have to atone for the murder with the life of a young heifer unspoiled by work under a yoke.
Moses didn’t know it, but what he really wanted was a Voronoi diagram.
The Voronoi diagram was named after Georgy Voronoy, who lived about 3,300 years after Moses and was thus a little too late to help. He also lived in Ukraine (then part of the Russian Empire) and thus a little too far away to help, too.
Despite the name, Voronoy didn’t actually invent the diagram. That was René Descartes, the one who invented the Cartesian geometry you learned in tenth grade and also the one who said, “I think, therefore I am”, but in Latin. Descartes did his work in 1644, a mere 3,100 years too late for Moses. Anyway, Voronoy laid down the modern definition of the diagram, and he generalized it into more than two dimensions. Mathematicians love generalizations, and they love higher dimensions, and so the diagram is named Voronoi even though he was 200 years late.
Here we sit in 2021, another 200 years too late to help, but let’s see if we can help anyway.
I picked an arbitrary map of Israel from roughly the time of Joshua, right after Moses gave the sermons recorded in Deuteronomy. I built a Voronoi diagram on top of it using the labeled cities as the points of interest.
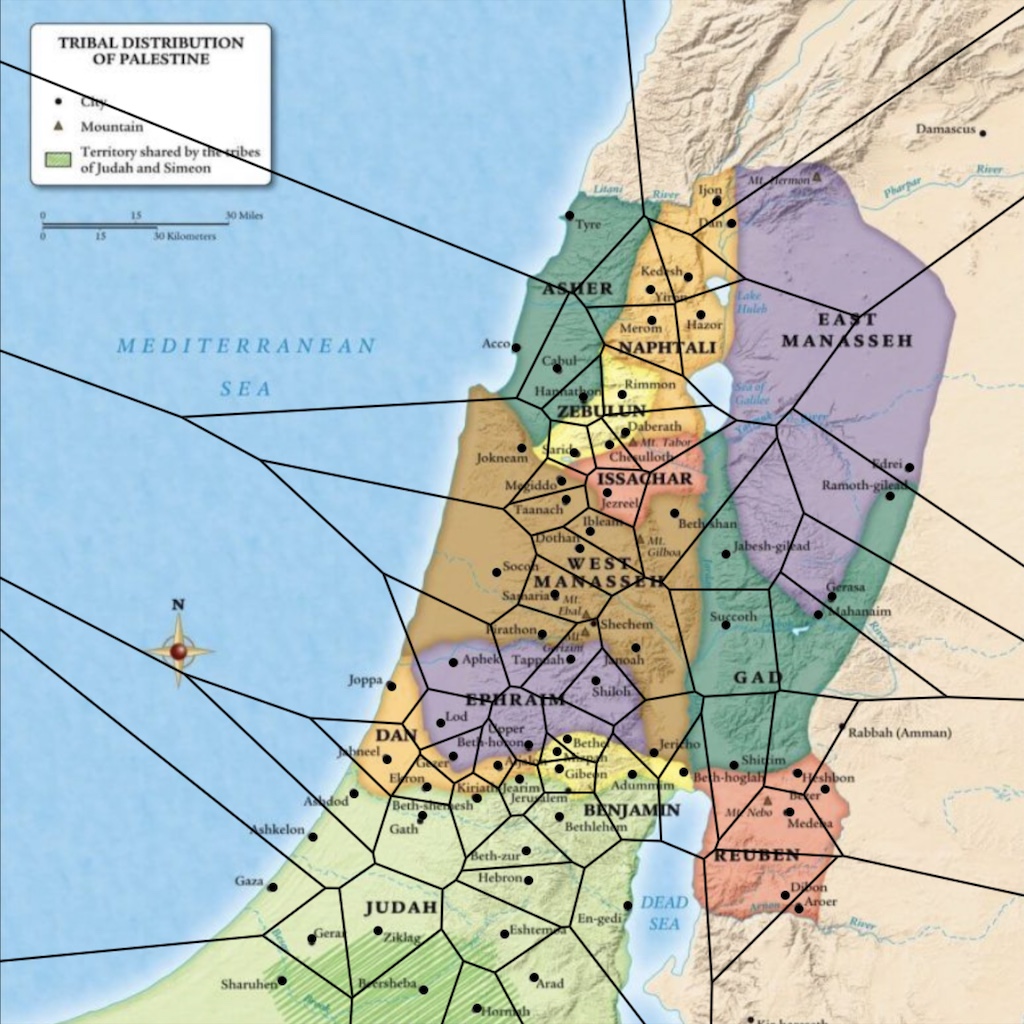
There! Now, any time a dead body is found, you just pull up the map, find where you and the body are, and then go get the elders of the city associated with your polygon. Easy-peasy.
Of course, I’ve ignored water boundaries and tribal boundaries, both of which would place realistic constraints on the calculations. For example, the majority of East Manasseh is actually closest to the cities of Hazor or Dan, but I doubt the people of Manasseh are likely to subject themselves to the elders of Naphtali, regardless of what Moses said.
There’s another problem with our map: there aren’t nearly enough cities on it. Presumably there were more than six cities in the territory of Gad, for example. The elders of Israel would have needed a much more dense map.
But it still would have helped.
Other Uses of the Voronoi Diagram
Other than helping satisfy Mosaic law from 3,500 years ago, what good are Voronoi diagrams?
It turns out there are many, many applications in the sciences, engineering, and math. For example, some biological and chemical processes appear to follow Voronoi diagrams (they’re probably not as colorful as the first image above, though).
But perhaps the coolest part of the Voronoi diagram is that every polygon is convex, meaning that you can draw a straight line from any point in it to any other point in it, and the line will never go outside the polygon. Go ahead, try it.
This fact makes all kinds of algorithms easier, and higher-dimensional geometries turn out to be fantastic structures for various computational optimization and machine learning techniques. There’s an entire field of math called “convex optimization” that is used all the time in applications from routing UPS deliveries to investment banking.
There are other neat properties of the Voronoi diagram. Here’s one you may already be wondering about, especially if you did like I suggested and started drawing lines on your map.
What happens if you draw lines connecting each pair of cities in adjacent polygons?
It’s kind of unexpected, given the weird shapes you started with: you end up with triangles. Lots and lots of triangles, and no other shapes. This thing you’ve created is called the Delaunay Triangulation of those points, named after yet a third guy who was way too late for Moses: Boris Delaunay, who published the relevant work in 1934.
Here, check it out:
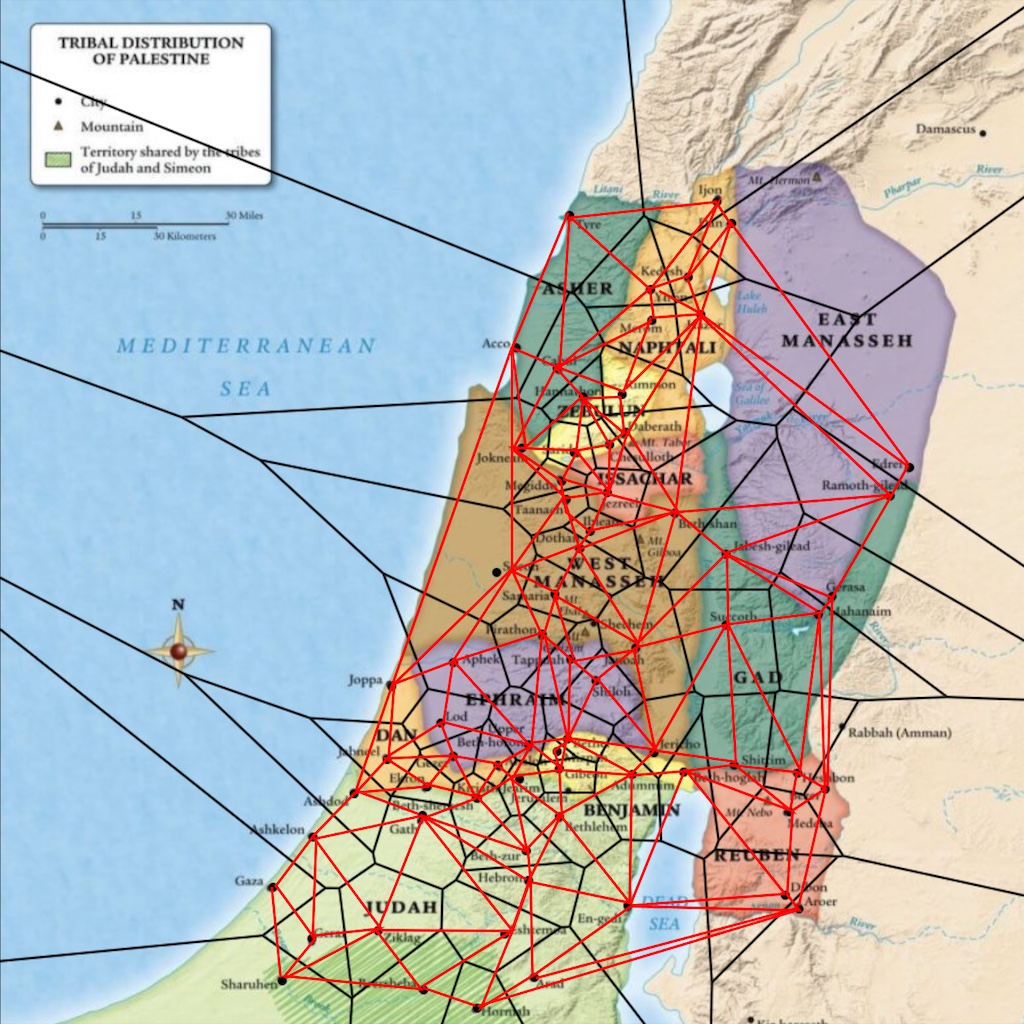
The Voronoi diagram is still shown in black, but the Delaunay Triangulation has been superimposed in red (by me, by hand, so there are some inaccuracies).
This map wouldn’t have helped Moses, but it would make computational geometers and video game designers very happy.
Wait. Video game designers?
I said before that convex shapes make a lot of kinds of math very easy, and this is why: triangles are the most convex shape, because they can never be anything else. A triangle is either convex or it’s not a triangle1. Triangles are also very easy to divide into smaller shapes, which are always also triangles.
Like I said, convenient.
One group of people who really love triangles like this are video game graphic artists (also special effects artists for movies, for the same reason). Every graphic you see in modern video games is made up of millions of triangles all rendered and shaded and colored and textured and lit so that they look like race cars or Master Chief. Even Minecraft, which looks like it’s made of cubes, is actually made of triangles arranged to look like cubes to you. It’s just easier.
The Delaunay Triangulation has another neat property, which is that these triangles are extremely triangular triangles. In fact, they’re the most triangular triangles that can possibly connect all these dots.
By “most triangular,” I mean “closest to an equilateral triangle.” The narrower a triangle gets, the less it looks like a triangle, don’t you agree? If you don’t believe me, take a fresh copy and see if you can connect the dots with better triangles. I’ll wait.
Back so soon? Anyway, because these are the most triangular triangles, they’re also the easiest for computers to work with when programming Assassin’s Creed: Conquest of Canaan2.
Getting to Delight
If you can’t tell, I am absolutely giddy about finding a Voronoi diagram in Scripture. I’m diving around in this passage like Scrooge McDuck in his coins.
Which is exactly how you’re supposed to enjoy Scripture. Like a duck. In coins3.
But if you’re still with me and also wondering what all this math has to do with the unfathomable glory of God and the ineffable meaning of the Scriptures and the incomparable beauty of Jesus, I completely understand, and I’m here to help.
There are two answers that are going to sound like cop-outs, but I don’t want to skip over them, because they’re important.
First, not every bit of Scripture will be as rich for every person who reads it. Maybe you geek out over how the call-and-response structure in Psalm 136 continues in today’s worship music. Maybe someone else always loses themselves in the emotion of Jeremiah’s Lamentations. And maybe I write 1,400 words about math inspired by God’s rules for maintaining the innocence of a nation when a man is found dead.
That’s okay, and expected, and good.
It means you can teach me about the psalms, and the other person can help me feel the loss of exile, and I can tell you why Moses would have benefited from a branch of mathematics invented more than three millennia after he died.
Second, Paul writes in Romans 12:15, “Rejoice with those who rejoice.” When someone else loves a bit of God’s Word enough to tell you about it, even if you don’t get why they’re so excited, you can share their joy. And in their joy, you can see a bit of the beauty and glory of God that you may not have seen before.
Okay, Sunday School answers, correct and true, are out of the way. Here’s the answer I really want to give.
The exploration of the natural world is the God-given responsibility of humanity.
Understanding why things happen the way they happen is a movement of God in the lives of mathematicians and scientists as much as poets and painters.
Solomon writes in Proverbs 6:6, “Go to the ant…consider her ways, and be wise.” He found wisdom in entomology.
The psalmist tells us, “Great are the works of the Lord, studied by all who delight in them.” (Psalm 111:2) Possibly a different psalmist tells us, “The heavens are telling of the glory of God; their expanse is declaring the work of His hands.” (Psalm 19:1)
If you want to understand the fullness of God, you will explore every nook and cranny of His work that you can get your hands on.
This… well, this is my nook. And I want to share my delight with you.